Pressure drop is decrease in pressure from one point in a pipe or tube to another point downstream. Pressure drop occurs due to frictional forces acting on a fluid as it flows through the tube. The frictional forces are caused by the resistance to flow. The main determinants of resistance to fluid flow are fluid velocity through the pipe and fluid viscosity. Any liquid or gas will always flow in the direction of least resistance (less pressure). Pressure drop increases proportional to the frictional shear forces within the piping network. A piping network containing a high relative roughness rating as well as many pipe fittings and joints, tube convergence, divergence, turns, surface roughness and other physical properties will affect the pressure drop. High flow velocities and / or high fluid viscosities result in a larger pressure drop across a section of pipe or a valve or elbow. Low velocity will result in lower or no pressure drop. Pressure Drop can be calculated using two values: the Reynolds Number, Re (determining laminar or turbulent flow), and the relative roughness of the piping.
Where D is the diameter of the pipe, v is the velocity of the fluid, ρ is the density of the fluid, and μ is the dynamic viscosity of the fluid. The relative roughness of the piping is usually known by cross referencing the Reynolds number with the relative roughness, the friction factor, f, is calculated.

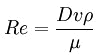
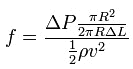
The velocity of hydraulic fluid through a conductor (pipe, tube or hose) is dependent on flow rate and cross sectional area. Recommended fluid velocities through pipes and hoses in hydraulic systems are as follows:

Service	Velocity (ft/sec)	Velocity (m/sec)
Pump suction	2-4	0.6 - 1.2
Pump return	4 - 13	1.5 - 4
Pump discharge	7 - 8	2 - 5.5

Use values at the lower end of the range for lower pressures or where operation is continuous. Refer to the flow/velocity nomograms for more information.

Alternatively, fluid velocity can be calculated using the following formula:
       Q × 0.408
v = --------------
           D²
Where:
v = velocity in feet per second (ft/sec)
Q = flow rate in US gallons per minute (US gpm)
D = inside diameter of pipe or hose in inches (in).

Calculation of Pump Head: Friction between the fluid flowing through a conductor and its inside wall causes losses, which are quantified as pressure drop. Pressure drop in conductors is an important consideration for the designer especially in systems where long pipe or hose runs are necessary. The pressure drop over a length of pipe or hose can be calculated using the following formula, which for ease of calculation uses metric units.
Before proceeding to the pressure drop calculations, the following variables need to be known:
Flow rate in liters per minute (L/min) Q
Inside diameter of pipe or hose in millimeters (mm) D
Kinematic viscosity of fluid (at operating temperature) in centistokes (cSt) ν
Density of the fluid in kilograms per cubic meter (kg/m³) ρ
Length of the pipe, tube or hose in meters (m) L

1. Calculate fluid velocity:
       Q × 21.22
v = --------------
           D²
                      
Where:
v = velocity in meters per second (m/sec)
Q = flow rate in liters per minute (L/min)
D = inside diameter of pipe or hose in millimeters (mm).
2. Calculate the Reynolds Number (Re):
       1000 × v × D
Re = -------------
           ν
                      
Where:
Re = Reynolds Number
v = velocity in meters per second (m/sec)
D = inside diameter of pipe or hose in millimeters (mm)
ν = kinematic viscosity of fluid (at operating temperature) in centistokes (cSt) 3. Calculate the friction factor (f)
The formula used to calculate the friction factor is dependent on the magnitude of the Reynolds Number. If the Reynolds Number is less than 2300, flow is laminar and the following formula is used to calculate the friction factor:
       64
f = -----------
           Re                      
Where :
f = friction factor
Re = Reynolds Number < 2300

If the Reynolds Number is between 2300 and 4000, flow is transition and greater than 4000 flow is turbulent. For Reynolds Numbers greater than 2300 and less than 100,000 the following formula can be used to calculate the friction factor:
f = 0.3164 × Re^-0.25
                      
Where:
f = friction factor
Re = Reynolds Number > 2300 and < 100,000
In instances where the Reynolds Number is greater than 100,000, friction is highly dependant on the roughness of the conductor inner surface. In these cases Colebrook equation, which considers pipe roughness, is used to calculate the friction factor. However, due to the relatively low fluid velocities and high fluid viscosities present in hydraulic systems, Reynolds Numbers of this magnitude should not be encountered.
4. Calculate the pressure drop:
Finally, pressure drop can be calculated using the following formula:
           v² × f × L × ρ
Δp = ----------------
                   2D
                      
Where:
Δp = pressure drop in Pascals (Pa)
v = velocity in meters per second (m/sec)
f = friction factor
L = length of pipe or hose in meters (m)
ρ = density of the fluid in kilograms per cubic meter (870-890 kg/m for hydraulic oil)
D = inside diameter of pipe or hose in meters (m)

Type of Fitting	K Factor
90 Deg Elbow Standard	0.5
90 Deg Elbow Single Miter	1.4
90 Deg Elbow Double Miter	0.8
90 Deg Elbow Triple Miter	0.6
45 Deg Elbow Standard	0.3
45 Deg Elbow Single Miter	0.5
Tee Straight flow	0.4
Tee flow to branch	1.4
Tee flow from branch	1.7
Reducer, Single reduction	0.7

When more accuracy is required, head loss in fittings can be determined using loss coefficients (K-factors) for each type of fittings. In this approach K-factor is multiplied by the velocity head of the fluid flow.
H = K (v²/2g)
where,
H = Head loss, m
V = Velocity of flow, m/s
Pressure drop or head loss, occurs in all piping systems because of elevation changes, turbulence caused by abrupt changes in direction, and friction within the pipe and fittings. The most common methods used to determine the head loss in fiberglass pipe are Hazen-Williams, Manning and Darcy-Weisbach equations. The suitability of each method depends on the type of flow (gravity or pumped) and the level of accuracy required. Due to the smooth inside surface and the resistance to corrosion, ADPF fiber glass pipes have a relatively low head loss as compared to other material pipes.
Hazen-Williams Equation: The Hazen-Williams Equation is applicable to water pipes under conditions of full turbulent flow. It has gained wide acceptance in the water and wastewater industries because of its simplicity.
v = 0.85 C R^0.63J^0.54
where,
v = velocity, m/s
C = Hazen-Williams Coefficient
R = Hydraulic mean radius, m
J = Hydraulic gradient, m/m
Hazen-William coefficient, C for ADPF fiber glass pipe is taken as 150.
Manning Equation: The Manning equation typically solves gravity flow problems where the pipe is only partially full and is under the influence of an elevation head only.
v = (1/n) R^0.667 J^0.5 where,
v = velocity, m/s
n = Manning Coefficient
R = Hydraulic mean radius, m
J = Hydraulic gradient, m/m
Manning Coefficient, n for ADPF fiber glass pipe is taken as 0.01
Darcy-Weisbach Equation: It states that pressure drop is proportional to the square of the velocity and the length of the pipe. This equation is valid for all fluids in both laminar and turbulent flow. The disadvantage is that the Darcy- Weisbach friction factor is a variable. J = ( f.L.v²)/2.g.D where,
J = Head loss, m
g = Gravity constant, 9.81 m/s²
v = Velocity, m/s
D = Inside diameter, m
f = Friction factor
L = Length of the pipe, m
The well known Reynolds number equation is used to characterize the fluid flow.
If the flow is Laminar,
f = 64 / Re
If the flow is Turbulent, the friction factor can be determined from the Moody diagram found in most fluid mechanics texts or calculated from the Colebrook equation.

Pressure drop in fittings: Head Loss in Fittings is frequently expressed as the equivalent length of pipe that is added to the straight run of pipe as shown below. This approach is used most often with the Hazen-Williams or Manning equations. The approach does not consider turbulence and subsequent losses created by different velocities.

Fitting mm NB	150	200	250	300	350	400	450	500	600	700	800	900	1000
90 Deg Elbow	8.5	6.4	7.9	9.4	10.7	12.2	14.0	17.0	23.0	28.0	32.4	37.1	42.3
45 Deg Elbow	3.5	3.4	4.2	5.0	5.7	6.5	8.2	10.9	13.6	16.2	20.1	23.5	25.6
Tee	11.0	14.4	17.8	21.1	24.0	27.5	32.8	38.3	49.5	61.5	72.9	84.6	96.8

Surge pressure (Water Hammer): Pressure surge or Internal shock, known commonly as water hammer, results from abrupt change of velocity within the system. Under certain conditions, these shock forces can reach magnitude sufficient to rupture or collapse a piping system, regardless of the material of construction. The transient pressure is the rapidly moving wave which increases and decreases the pressure in the system depending on the source of the transient and direction of wave travel. Rapid valve closure can result in the build-up of shock waves due to the conversion of kinetic energy of the moving fluid to potential energy which must be accommodated. These pressure waves will travel throughout the piping system and can cause damage far away from the wave source. The magnitude of the water hammer depends on

• Fluid properties
• Velocity of flow
• Modulus of Elasticity of the pipe material
• Length of the pipe line
• Speed in which the momentum of the fluid changes

The low modulus of elasticity of fiberglass contributes to a self dampening effect as the pressure wave travels through the piping system. The magnitude of pressure wave in a metallic piping system is much higher due to the higher modulus of elasticity of these materials. In addition to rapid valve closure or opening, sudden air release and pump start up or shut down can create water hammer. Talbot formula gives:

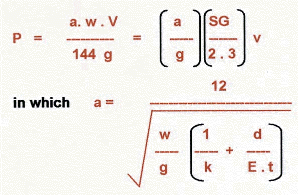
where,
a = Wave velocity (ft/s)
P = Surge Pressure (psi)
v = Change in flow velocity (ft/s)
w = Density of fluid (lb/ft³)
SG = Specific gravity of fluid
K = Bulk modulus of fluid (psi)
E = Hoop modulus of elasticity (psi)
d = Inside diameter of pipe (inch)
t = Pipe wall thickness (inch)
g = Acceleration due to gravity (ft/s²)
Good design practice usually prevents water hammer in most systems. Installation of valves which cannot open or close rapidly is one simple precaution. In addition, pumps should never be started into empty discharge lines unless slow opening mechanically actuated valves can increase the flow rate gradually. Check valves on pumps should close as quickly as possible to minimize the velocity of fluid flowing back. In some cases, thoroughly anchoring the piping system may mitigate this problem. In other cases, mechanical valve operators, accumulators, or feedback loops around pumps may have to be used to remove the source of water hammer.